Hypotheses Testing Strategy
By M-Estimator January 5, 2020
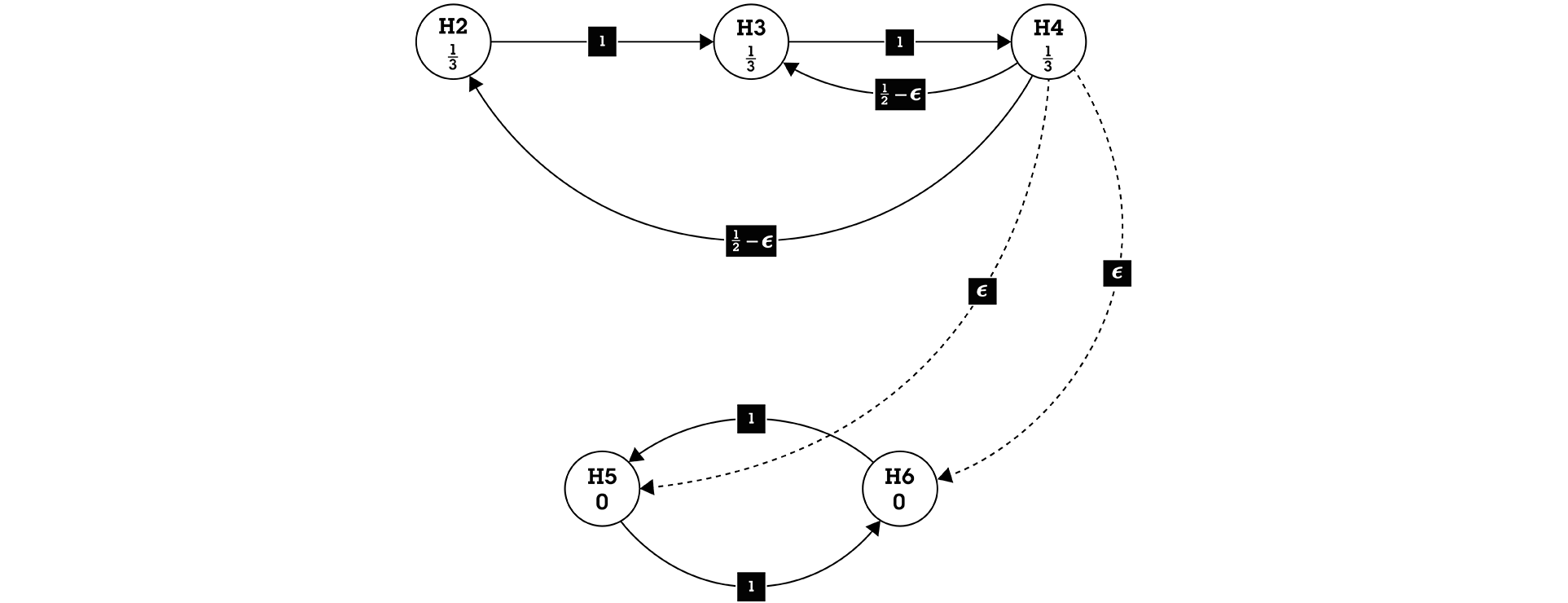
Figure 1 Closed Testing Procedure for Secondary Family
An Illustration of a
Hypotheses Testing Strategy
In testing multiple hypotheses, control of the study-wise error rate should be considered. As the number of statistical tests within a trial increases (multiplicity), the chance of making a false conclusion (false positive) about a drug’s effect with respect to at least one of the endpoints increases if multiplicity is not addressed. In this simulated clinical trial, there are three families of hypotheses, namely:
Primary family F1 = {H1}, H1 is the primary endpoint
Secondary family F2 = {H2, H3, H4, H5, H6}, H2, H3, H4, H5, H6 are the secondary endpoints
Exploratory family F3 = {H7 - H12}, where H7 - H12 denote the exploratory endpoints.
To control the study-wise, or experiment-wise Type-1 error rate at pre-specified level α =0.05, a gate-keeping strategy (or serial strategy) will be employed. The primary family (F1) will be tested first, and then the secondary family (F2) contingent upon the results within the primary family, and finally the exploratory family (F3) will be tested dependent upon the results within the secondary family. This approach is called the gatekeeping testing strategy to highlight the fact that the endpoint families are analyzed in a sequence, with each family serving as a gatekeeper for the next one. The tests for the secondary family (and subsequent families) are carried out with appropriate multiplicity adjustments within that family, but only if the tests in the primary family have been successful.
The primary endpoint is the most important endpoint of this study. Thus, the statistical plan is to assign the total available alpha (α= 0.05) to F1 and test the endpoint H1 at alpha level of 0.05. No alpha is reserved for the second family. The second family is tested using a weighted Bonferroni-Holm sequentially rejective multiple testing procedure at full alpha of 0.05, if and only if the primary endpoint is significant. This procedure will pass alpha from the secondary family to the exploratory family only when all the null hypotheses in the secondary family are rejected.
If all endpoints in F2 are significant, then the exploratory family (F3) will be tested using a similar procedure. Testing for the secondary family and exploratory family (not shown) can be illustrated using the graphical approach. Below we describe the strategy for the tests of hypotheses.
Primary family:
Test the primary endpoint (H1) at the total available alpha, α= 0.05, if significant, then proceed to testing the secondary family.
Secondary family:
For the improved fallback method, testing proceeds in a sequential fashion, with the distinction that the local α can accumulate if hypotheses are rejected, thereby allowing higher power for later hypotheses. Please see Figure 1 for an illustration.
Test the three null hypotheses, H2, H3, and H4. Each of the hypotheses is assigned its associated local significance level α/3=0.0167. If H2 is rejected, then the level α/3 is carried over to H3, as indicated by the edge pointing from H2 to H3 and tested at the local significance level (α/3+ α/3 = 2α/3), otherwise, if H2 is not rejected, then H3 tested at α/3. If H3 is rejected at the local significance level (either α/3, or 2α/3), then that level is carried over to H4, as indicated by the edge pointing from H3 to H4. In the case for which H2 and H3 are both rejected, H4 is tested at full alpha of 0.05.
We use the concept of infinitesimal small weight. In the case for which H2 (H3) are not rejected, and H4 is significant, almost all its local significance level α/3 (except an infinitesimal small amount) is split into half and passed on to H2 (H3) as indicated by the directed edges with weights ½- ε. Here, ε (epsilon) denotes an infinitesimally small weight, indicating that the significance level is carried over from H4 to (H5 - H6) only if all three hypotheses, H2, H3, and H4 are rejected. Note H5 and H6 have no assigned significance level.
If and only if H2, H3, and H4 are all rejected, then H5 and H6 are tested. Hypotheses H5 and H6 are tested simultaneously at the inherited local significance level of α/2= 0.025. If H5 (H6) is rejected at its local significance level (α/2), this level is passed to H6 (H5) as indicated by the directed edges with weights 1.
Exploratory family:
If all endpoints are rejected from the secondary family, then the exploratory family (F3) which contains several hypotheses (H7 - H12) can be tested (strategy not shown).
There are indeed arguments for, and against, combining F2 with F3 as one secondary hypothesis family. Statistical science is not only a rigorous scientific discipline, but as well, an art.
References:
1. Dmitrienko A, Offen W, Westfall P. Gatekeeping strategies for clinical trials that do not require all primary effects to be significant. Stat Med (2003) 22:2387–400. doi:10.1002/sim.1526
2. Wiens BL, Dmitrienko A. The fallback procedure for evaluating a single family of hypotheses. J Biopharm Stat 2005;15:929-942
3. Bretz F, Maurer W, Brannath W, Posch M. A graphical approach to sequentially rejective multiple test procedures. Stat Med (2009) 28:586–604. doi:10.1002/sim.3495
4. Wang B and Ting N (2014) An application of graphical approach to construct multiple testing procedures in a hypothetical phase III design. Front. Public Health 1:75. doi: 10.3389/fpubh.2013.00075

